Nonlinear Programming 

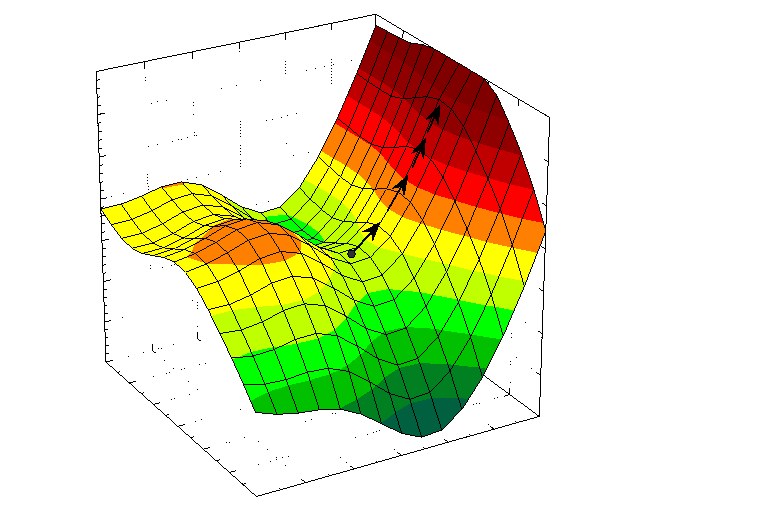
A typical difficulty associated with nonlinear optimization is the problem that in most cases it is only possible to determine a locally optimal solution but not the global optimum. Loosely speaking, the global optimum is the best of all possible values while a local optimum is the best in a nearby neighborhood only.

Algorithms to Solve NLP Problems

Algorithms to solve NLP problems are found for instance in Gill et al. (1981) or Fletcher (1987). Most of them are based on linearization techniques. Inequality conditions are included for instance by applying active sets methods. The most powerful nonlinear optimization algorithms are the Generalized Reduced Gradient algorithm (GRG) and sequential quadratic programming (SQP) methods. The GRG algorithm was first developed by Abadie and Carpenter (1969) [more recent information is contained in Abadie (1978), Lasdon et al. (1978) and Lasdon and Waren (1978)]. For NLP problems with only a few nonlinear terms and in particular NLP problems containing pooling problems recursion or  is frequently used.